@mau @matematica C’è qualcosa che non mi torna, di numeri primi di quella forma ce ne sono, per esempio 140001089, 1401099989 e 14000109989.
Ma poi 57p si intende 57 seguito dalla stringa delle cifre di p oppure è una moltiplicazione?@enzotib
Infatti nella lista OEIS ci sono7980062073 = 57·140001089;
79862699373 = 57·1401099989; e
798006269373 = 57·14000109989.Per altro la seguente riga per GP-Pari[*]
for(i=0,20,for(j=2,22,p=11*(10j-1)+14*10(j+3+i);if(isprime(p),print(p))))
ne ha trovati una trentina in 163 millisecondi.
Magari non è facile dimostrare che non ce ne sono altri in mezzo tra i sette della lista OEIS e quelli che si possono trovare in questo modo…
[*] https://pari.math.u-bordeaux.fr/
@mau @matematica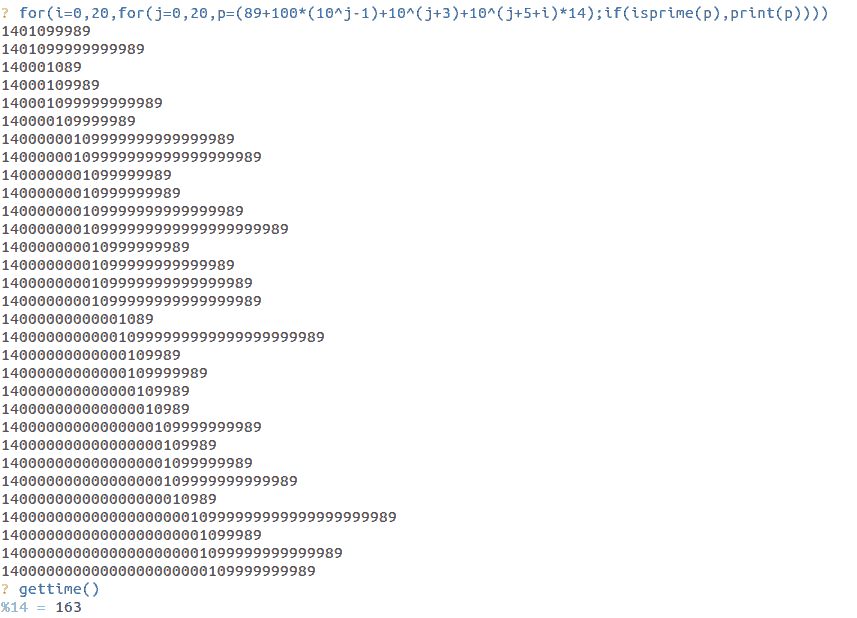
deleted by creator
@enzotib io sono partito da https://jlpe.tripod.com/ppn/ppn.htm . Ma che c’entrano i numeri primi? È vero che avevo sbagliato a fare l’esempio (ora è corretto), ma l’unico divisore proprio di 140001089 è 1 e quindi la somma dei divisori scritti alla rovescia è 1, non 980100041.
57p è una moltiplicazione.
deleted by creator
@Pare no, hai ragione. Non fanno parte della lista perché non sappiamo se ce ne sono altri!



